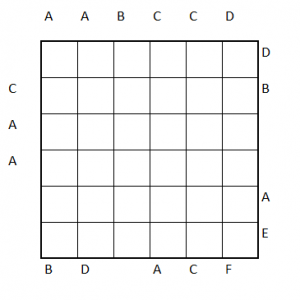
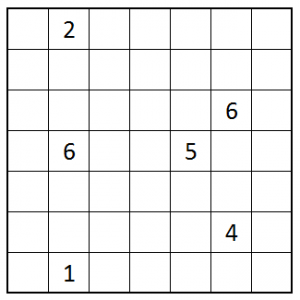
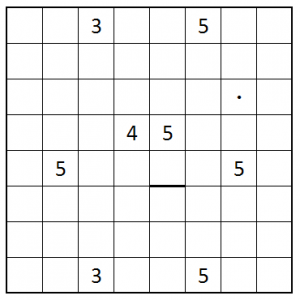
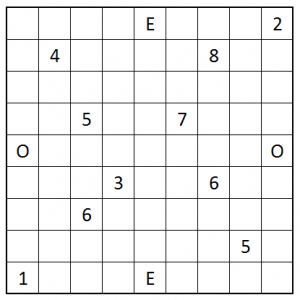
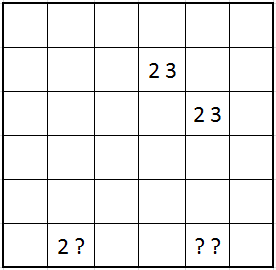
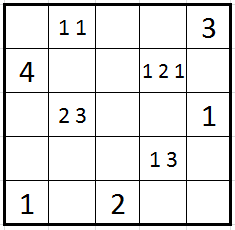
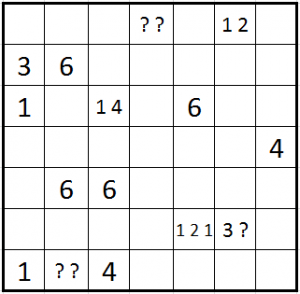
Star Tours
I appear to be in the mood for Star Battle derivatives.
I haven’t seen this kind of puzzles anywhere else, so I named it “Star Tour”. As weird as Star Battle, in my opinion.
Rules:
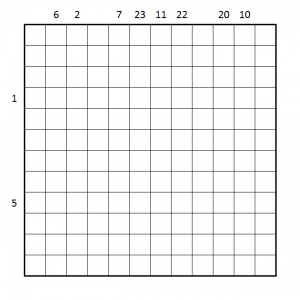
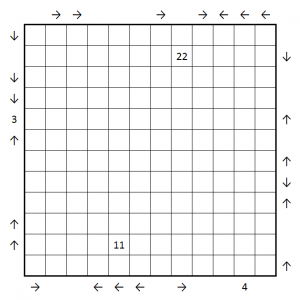
- Place two stars in every row and column such that no two stars touch each other, even by corners.
- The stars are numbered from 1 to 2n. Moving orthogonally from star to star in order must result in a loop that visits all stars. 2n loops back to 1.
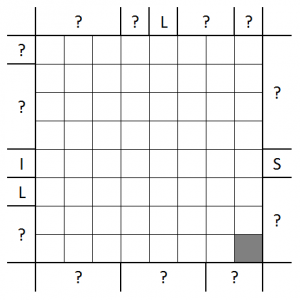
- A number along the edge of the grid tells the number of the star first seen on that row/column.
- An arrow along the edge of the grid tells the direction where the next star in sequence is looking from the star first seen on that row/column.
The first one is rather easy, but the second one with the arrow clues is tricky.