©2012-2013 Perplexible
All Rights Reserved.
Designed by David Millar
Here’s two Skyscrapers. Every letter stands for a different number. Ranges are 1-5 and 1-6 respectively.
If I hypothetically had to say something about their difficulty, I suppose they aren’t hard. Both have a spot where you have to pause and think, but other than that things flow smoothly. That seems to be common in my puzzles.
Here’s some Linesweeper puzzles (the puzzle style was invented by Jak Marshall).
The 7×7 one is an easy starter.
I (hopefully) fixed the ambiguity issue with the 8×8 one. It might be easier but it’s also nicer now, I think. The loop can’t cross the bold line and it has to visit the dotted square.
The 9×9 one is tricky. It has clues from 1 to 8, with 5 and 6 doubled. O means the clue is odd, E means the clue is even.
It’s a mashup of Easy as ABC and regionless LITS.
Standard regionless LITS rules:
Additionally:
Hopefully I was clear with the rules.
This one took a bit of wrangling to make it work, because I insisted on having the diagonal read 1-2-3-4-5 whle keeping it litsable. Anyways, I like how it turned out.
Rules: It’s a Nurikabe. It’s also a borderless LITS; or equivalently, the filled area must be tileable with tetrominoes such that no two of the same shape share an edge. Lastly, the numbers outside the grid tell how many tetrominoes are in that row/column.
5th (!) post in a row…
This is a straightforward hybrid of Star Battle and Galaxies.
The centers of every galaxy are marked on the grid. The galaxies all have two-fold (180°) rotational symmetry.
Each galaxy has either two stars or no stars. The stars need not be symmetrically placed. A black dot indicates that the galaxy has two stars in it, a crossed out white dot indicates that the galaxy has no stars. Normal white dots can be either.
Additionally, every row and column has two stars in it, and the stars don’t touch even diagonally.
Slither Tapa plays like a mix of Slitherlink and Tapa. The continuous area inside the slither is shaded. Unshaded numbers are Tapa clues, shaded numbers are Slitherlink clues.
EDIT: Apparently also known as Tapa Rundweg or Loop Tapa (but not to be confused with Tapa Loop… :p).
They may not be that hard but I had fun making them.
One more! 😀
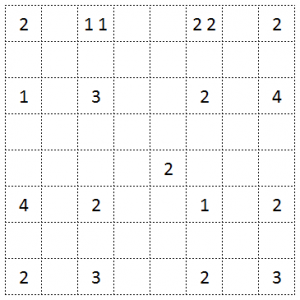
This time, Tapa puzzles! I quite like them, I’d describe Tapas as a mix of nonograms and minesweepers. See the link for instructions.
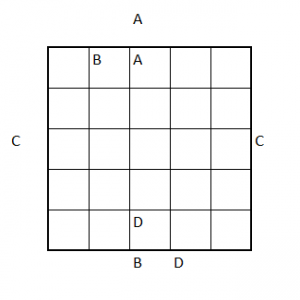
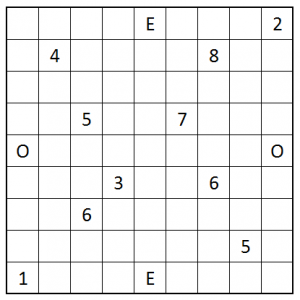
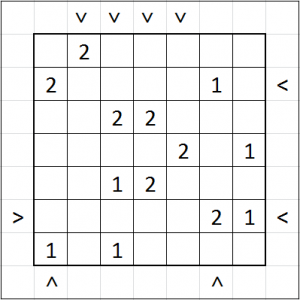
Here’s a slight variant. Plays like Tapa, but with added restrictions:
– Every column must have a different amount of filled tiles
– Every row must have a different amount of filled tiles
That doesn’t mean a row and a column can’t have the same amount of filled tiles.
(This variant is called Tap Differently in the puzzle app mentioned in my previous post.)
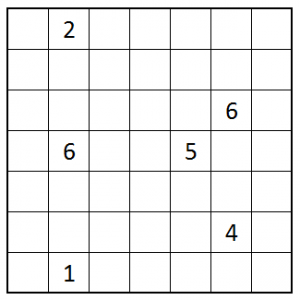
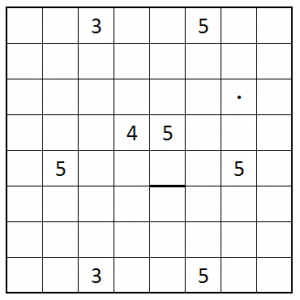
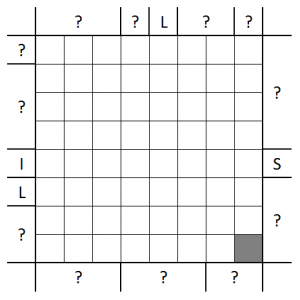
Now for the main course. I don’t know if this variation is unique but I haven’t seen any before. I’ve named them Yin Yang Tapas. (Feel free to suggest a better name in the comments.)
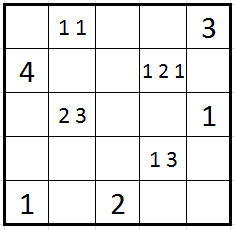
It’s a stronger variation on Tapa. Now even the numbered tiles may be filled!
– If a numbered tile is not filled, it tells you the amount of filled tiles around it, like Tapa.
– However, if a numbered tile is filled, it tells you the amount of empty tiles around it.
Otherwise it follows the rules of Tapa: that is, there are no 2×2 squares of filled tiles and the filled area is continuous.
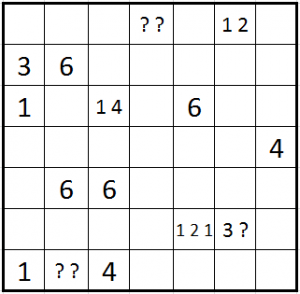
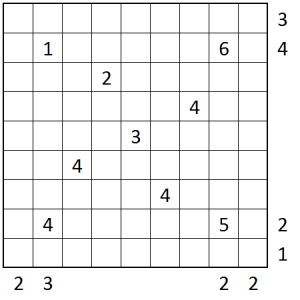
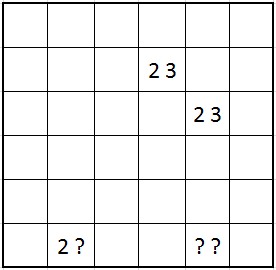
Here’s a 7×7 one.
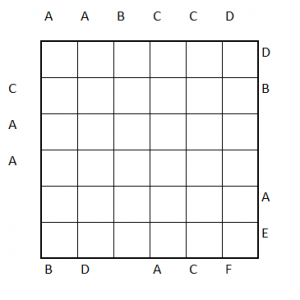
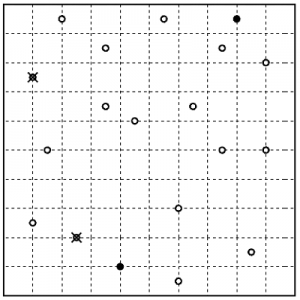
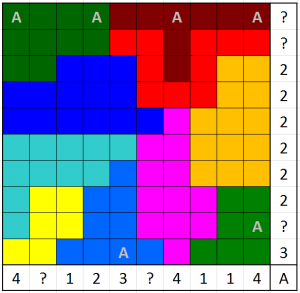
Neither are particularly hard. In any case, here’s the solution to the 5×5 Yin Yang Tapa, if you want to check that you understood the rules. Viewer discretion advised.
Double-posting because why not?
Here’s a puzzle I devised roughly half a year ago. It’s nice to be able to post it somewhere!
It’s a hybrid of Parks and Tents (both as seen in this excellent free puzzle app for iPhone (I sadly get no money for mentioning it as far as I know)). I haven’t seen any Parks puzzles outside that app, if anyone can link some I’d like that.
The goal is to fill the grid with tents and trees. The grid has six tents already placed, marked with A.
Like in Parks puzzles, the colored sections are parks. On each row, column and park are two trees. Trees may not touch each other, even diagonally.
Like in Tents puzzles, the numbers on the edges tell the amount of tents on that row. Tents may not touch each other, even diagonally, like trees. (The numbers include the pre-placed tents.)
Every tent attaches to one and only one tree. Every tree has one and only one tent attached to it. A tent and a tree can be attached to each other if they’re directly adjacent; touching diagonally won’t do. So, in practice, you’re placing pairs of tents and trees.
A tent and its tree need not be in the same park.
This is quite a tricky puzzle, I’m rather fond of it.
Hai everyone!
I haven’t seen any puzzles like this before, do comment if you have.
Outside the grid are laser emitters, marked with > .
The goal is to place mirrors inside the grid, according to the rules:
A mirror is placed diagonally inside a tile, reflecting the laser that hits it by 90 degrees (or pi/2 rad, if that’s your thing). The mirrors are double-sided, both sides reflect.
The numbered tiles tell both how many lasers pass through that tile and how many mirrors are adjacent to that tile (Minesweeper style).
Every mirror is hinted by a number; there are no hidden mirrors. Also, the mirrors may not be placed on numbers.
Every mirror must be hit by at least one laser.
Every laser must pass through at least one number. Lasers may not hit laser emitters.
Hopefully the rules are comprehendable!
ArDeeJ
chaotic_iak
ash
David Millar
krazydad
meanderlawn
Daniël Muilwijk
David Nacin
reesylou
rishipuri
Whit McMahan