Perplexible

I finally made a puzzle blog of my own. You can find it here: http://tspuzzles.wordpress.com/

I’ll be posting my puzzles mainly there from now on, but I might post one here every now and then.

Also, thank you Dave Miller for letting me in here in the first place.

See you!

Posted in Puzzle by ArDeeJ, 10/7/14 11:12 AM
No Comments »

Interested in the camaraderie of solving the daily crossword puzzle in the newspaper, but hate words and love numbers? There’s a Facebook group for you.

Every day, The League of Extraordinary Ladies and Gentlemen features a sudoku variant from one of a wide variety of talented sudoku authors around the world. Variants include simple changes to shapes and groups, non-standard clue types, and the occasional mathematics concept thrown into the mix.

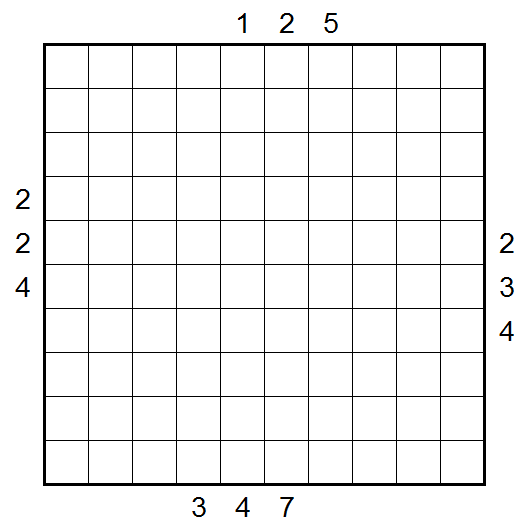
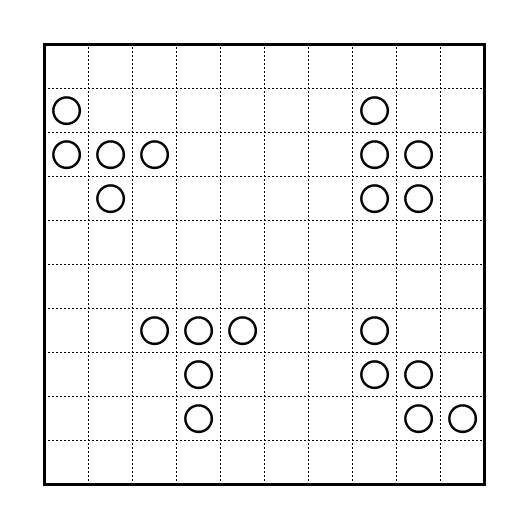
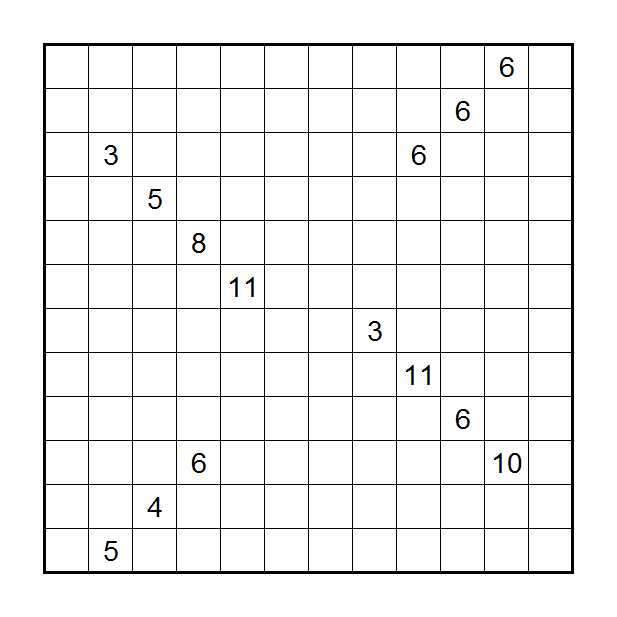
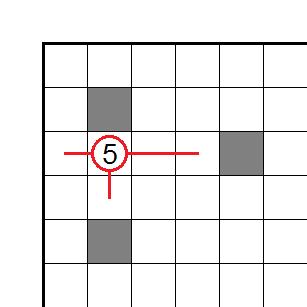
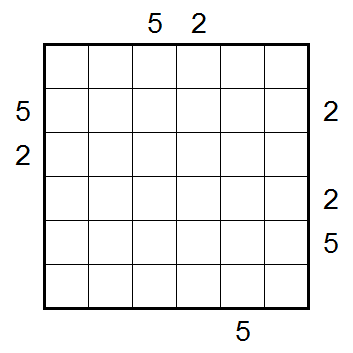
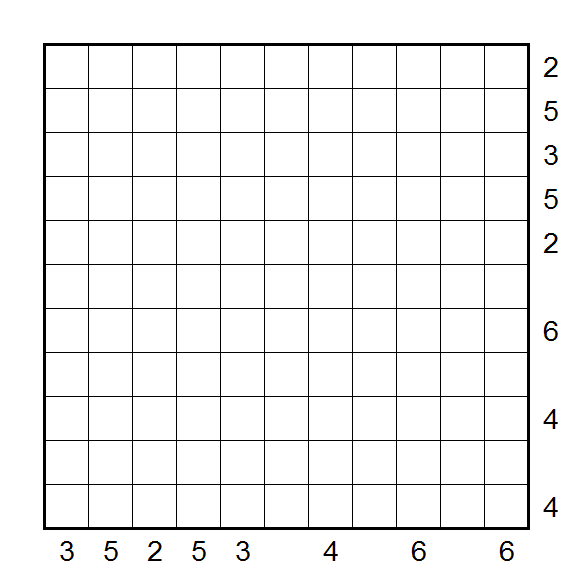
Unable to leave well enough alone, my last puzzle for the group included a wide variety of clue types. Shaded cells are even digits, plain cells are odd digits. Circle cells are the sum of the digits along their arrows. Numbers outside the grid are skyscraper clues.

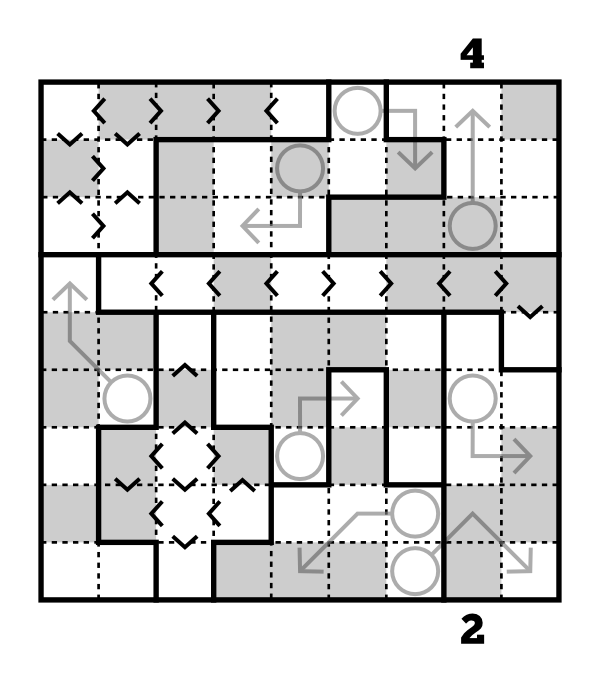
Word has it you can solve it without the skyscraper clues, but they certainly make it easier.

Posted in Puzzle, Sudoku, Sum Sudoku by David Millar, 10/4/14 9:35 PM
2 Comments »

This is already the fourth one of these I’ve made, which I consider a feat given how many of my puzzles tend to be one-shot variations.

Rules:

• Unlike in regular Nurikabe, the clue numbers have been placed outside the grid.
• A clue will appear in the first unshaded cell in its row/column, counting from the clue’s direction.
• Standard Nurikabe rules then apply:
  • Shade some cells to form a continuous wall that contains no 2×2 squares of shaded cells.
  • The clue numbers hint at connected groups of unshaded cells.
  • Every group has exactly one clue, which tells the group’s size.

Posted in Nurikabe, Puzzle by ArDeeJ, 10/4/14 8:25 AM
No Comments »

I’ve been wanting to make a Pentominous puzzle for a while, and this is the result. The puzzle has a shift in difficulty towards the end, and that’s because I wanted to stick to the theme, and got bored searching through the alternatives. I like it as it is, though.

I wouldn’t be surprised if this variant already has a name, if so please tell me in the comments.

Rules:

• Divide the grid into pentominoes (continuous shapes made out of five cells).
• No two pentominoes of the same shape may share an edge (even if they’re mirrored copies of each other), but touching by corners is allowed.
• Every pentomino must contain exactly one pearl.

Posted in Puzzle by ArDeeJ, 10/3/14 7:14 AM
2 Comments »

This one is a hybrid of Yajilin and Kuromasu (aka Kurodoko). It ended up a bit odd (the first iteration turned out to be broken, and fixing it altered the solving path), but I like it. Reminds me of my Crypto Regional Yajilin, actually.

Rules:

• Draw a loop passing through some of the cells, and shade the unvisited cells. The loop passes through the centers of cells, and makes right-angled turns.
• Two shaded cells may not share an edge, but touching by corners is allowed.
• A clue tells the total amount of consecutive horizontally or vertically connected unshaded cells (visited by the loop) connecting to the clue, counting the clue cell as well. Clue cells may not be shaded.

Put more concisely, it’s a Yajilin with Kuromasu clues (but the loop must visit all clue cells as well). This picture should clarify the cell counting rule:

EDIT: Clarified the rules. Unlike in Yajilin, the loop must visit all the clue cells as well, they may not be shaded.

Posted in Puzzle by ArDeeJ, 10/1/14 1:05 PM
2 Comments »

I realised I haven’t made a single vanilla Skyscrapers, so here’s one.

Rules:

• Fill the grid with numbers from 1 to 6 such that no number repeats within a row or column.
• The grid represents a top-down view of a city. A number in a cell represents a skyscraper of that height.
• A skyscraper blocks view of any shorter skyscrapers behind it.
• Looking from the clue’s direction, a clue tells the number of visible skyscrapers on its row/column.

Posted in Puzzle by ArDeeJ, 09/29/14 11:29 AM
No Comments »

Keeping in line with this week’s theme on the GMPuzzles blog, here’s another pentomino-based puzzle. Compared to today’s State Park variant, this is probably the easier of the two.

As you may guess, it’s a hybrid of Statue Park and Creek.

(click for full size)

Rules:

• Shade some cells (60, to be exact) to form the 12 given pentominoes, rotations and reflections allowed.
• No two pentominoes may share an edge, but touching by corners is allowed.
• The unshaded cells must form a single, connected region.
• A clue tells how many of the four cells around it are shaded.

Posted in Puzzle by ArDeeJ, 09/20/14 11:12 AM
4 Comments »

Whoops, sorry for the break in posting. University and whatnot.

Here’s a LITS variant: every region has two tetrominoes, instead of one. Other puzzles of this type seem to not allow tetrominoes in the same region to touch each other, but that restriction isn’t at play here.

(click for full size)

Rules:

• Shade some cells to form two tetrominoes in each region.
• Two tetrominoes of the same shape may not share an edge.
• The shaded cells must also form a connected wall that contains no 2×2 squares of shaded cells.

Posted in LITS, Puzzle by ArDeeJ, 09/15/14 9:29 AM
3 Comments »

Today’s puzzle is the second in an apparent series; that is, a series of not-quite-symmetrically clued Masyu variants. Here’s the first one, and it’s probably the harder of the two, at least if you’re trying to prove uniqueness. I quite like these both, which is why I’m publishing them in their faulty-symmetric glory. There’s also 6×6 starter, which showcases why I didn’t bother with colour antisymmetry.

Rules:

• Draw a single non-self-intersecting loop that runs through the centers of the cells and visits all pearls.
• On black pearls the loop must make a right turn, and the loop must go straight through the cells before and after the pearl.
• On white pearls the loop goes straight through, and the loop must make a right turn on at least one of the cells before and after the pearl.
• Additionally, every other pearl the loop passes through is a liar: that is, a white liar pearl acts as a black pearl, and vice versa.

Posted in Puzzle by ArDeeJ, 08/18/14 3:53 PM
2 Comments »

Here’s a Clouds puzzle.

Rules:

• Shade some cells to form rectangular clouds. The clouds don’t touch each other, even by corners.
• A cloud must be at least two cells tall and wide: 1×n or n×1 clouds aren’t allowed.
• The clues tell the amount of shaded cells in that row/column.

Posted in Puzzle by ArDeeJ, 08/14/14 12:26 PM
No Comments »