Perplexible

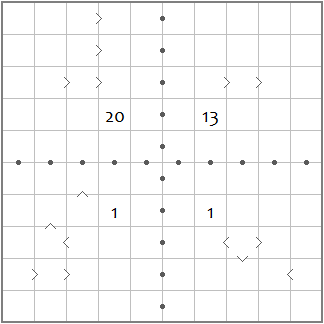
Fillomino Borders. Divide the grid into regions (polyominoes) such that no two regions with the same size touch orthogonally, and put a number in each cell describing the area of the region it is contained in. Additionally, some clues appear:
– Inequality signs must be satisfied by the numbers in the corresponding two cells pointed by the signs.
– Black circles indicate that one of the numbers among the two cells a circle touches is exactly twice the other number. (Kropki circles)
However, the converse doesn’t apply; not necessarily all inequality signs and black circles that can appear are present.

Answer key: Enter the contents of the eighth row (counting from top, describing from left to right), followed by a comma, followed by the contents of the eighth column (counting from left, describing from top to bottom). Only enter the units digit (the last digit) of each cell; for example, for a 10, enter 0.

A new year special of course, with the 2013-1-1 theme. But apparently it’s missed by one of my blog’s solvers. Ya, I forgot to schedule this post for Perplexible, I only remembered to schedule for my blog 😛

Posted in Puzzle by chaotic_iak, 01/2/13 3:31 AM
No Comments »

Yay first post by chaotic_iak *insert shameless advertising he– wait I already have*

To begin my double-posting adventure, I’ll crosspost my Puzzle 39 here.

Liar Slitherlink. Follow regular Slitherlink rules. In addition, exactly one number from each row/column is false.

Answer key: Enter the number of cells inside the loop in each row from top to bottom without separators. If there are 10 cells inside the loop, put 0.

Unlike in my blog (linked above), I will not write stories for each puzzle here. Go there for stories. I will also post a puzzle here only if I think it’s good. Well, this one is average in my current standards, but it’s a good introduction to my style of puzzles…maybe.

…or well, maybe I’ll post here more often, because I can’t have the fave/solved API in my WordPress blog. As you see above, I have an answer key here. Blah why I can’t have the API in my WordPress blog. *insert rant here*

Posted in Puzzle, Slitherlink by chaotic_iak, 12/11/12 2:10 AM
2 Comments »